总体分布，样本分布，抽样分布

Polulation, sample, and sampling distributions

# Population，总体
# 总体均值设置为100
miu <- 100
# 总体标准差设置为15
delta <- 15
# 随机种子值设置为20240906
set.seed(20240906)
# 生成10000个均值为miu、标注差为delta的IQ分数
IQ <- rnorm(10000, mean = miu, sd = delta)
# 生成10000个ID（被试编号）
ID <- seq(1:10000)
# 将ID与IQ存入数据表中
Population10000 <- data.frame(ID, IQ)
# 查看数据表
# View(Population10000)
# 查看数据表前6行
head(Population10000)

  ID       IQ
1  1 100.5975
2  2 121.5878
3  3 106.6454
4  4 111.8736
5  5 114.5555
6  6  77.9921

# 从总体中随机抽取一个样本量为100的样本，抽取其ID
sample1ID <- sample(Population10000$ID, 100)
# 根据ID选出sample1的数据
sample1 <- Population10000[sample1ID, ]
# 计算sample1的IQ的均值
sample1_mean <- mean(sample1$IQ)
sample1_mean

[1] 99.16138

# 计算sample1的IQ的标准差
sample1_sd <- sqrt(sum((sample1$IQ - sample1_mean)^2)/100)
sample1_sd

[1] 14.07578

# 基于sample1估计总体的标准差
sample1_sd_unbiased <- sqrt(sum((sample1$IQ - sample1_mean)^2)/(100 - 1))
sample1_sd_unbiased

[1] 14.14669

# 使用sd函数计算sample1的无偏标准差（总体标准差的估计值）
sd(sample1$IQ)

[1] 14.14669

# 从总数为10000的样本中累计抽取1000个样本量为100的样本，存入samples
set.seed(20240906)
samples <- list()
for (index in 1:1000) {
  samples[[index]] <- Population10000[sample(Population10000$ID, 100), ]
}
# 分别计算1000个样本的均值，一共得到1000个均值，存入samples_means
samples_means <- list()
for (index in 1:length(samples)) {
  samples_means[[index]] <- mean(samples[[index]]$IQ)
}
# 将samples_means转换为向量
samples_means <- unlist(samples_means)
head(samples_means)

[1]  99.48403  99.52555  99.94199  98.66905 101.19954 101.14274

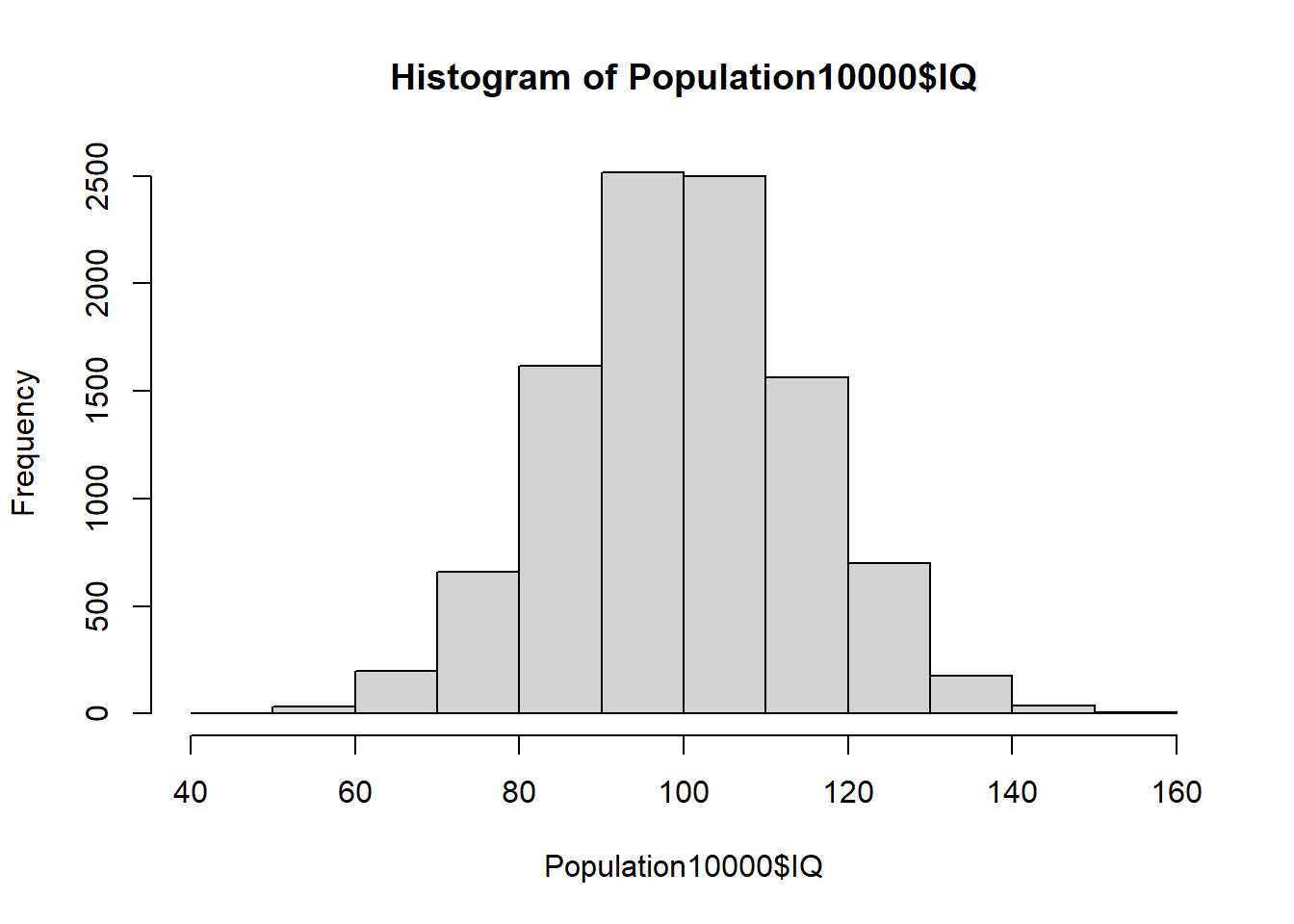
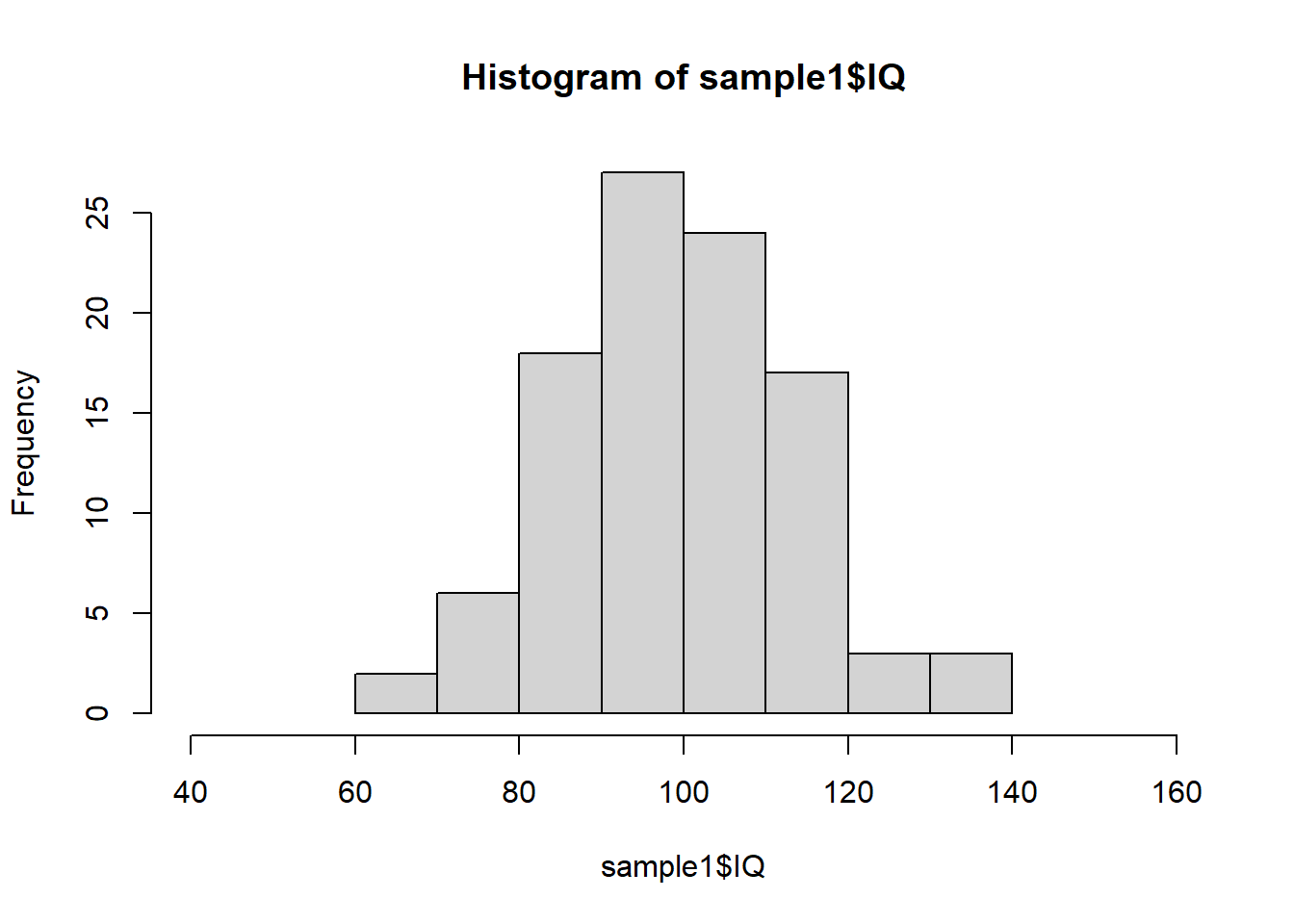
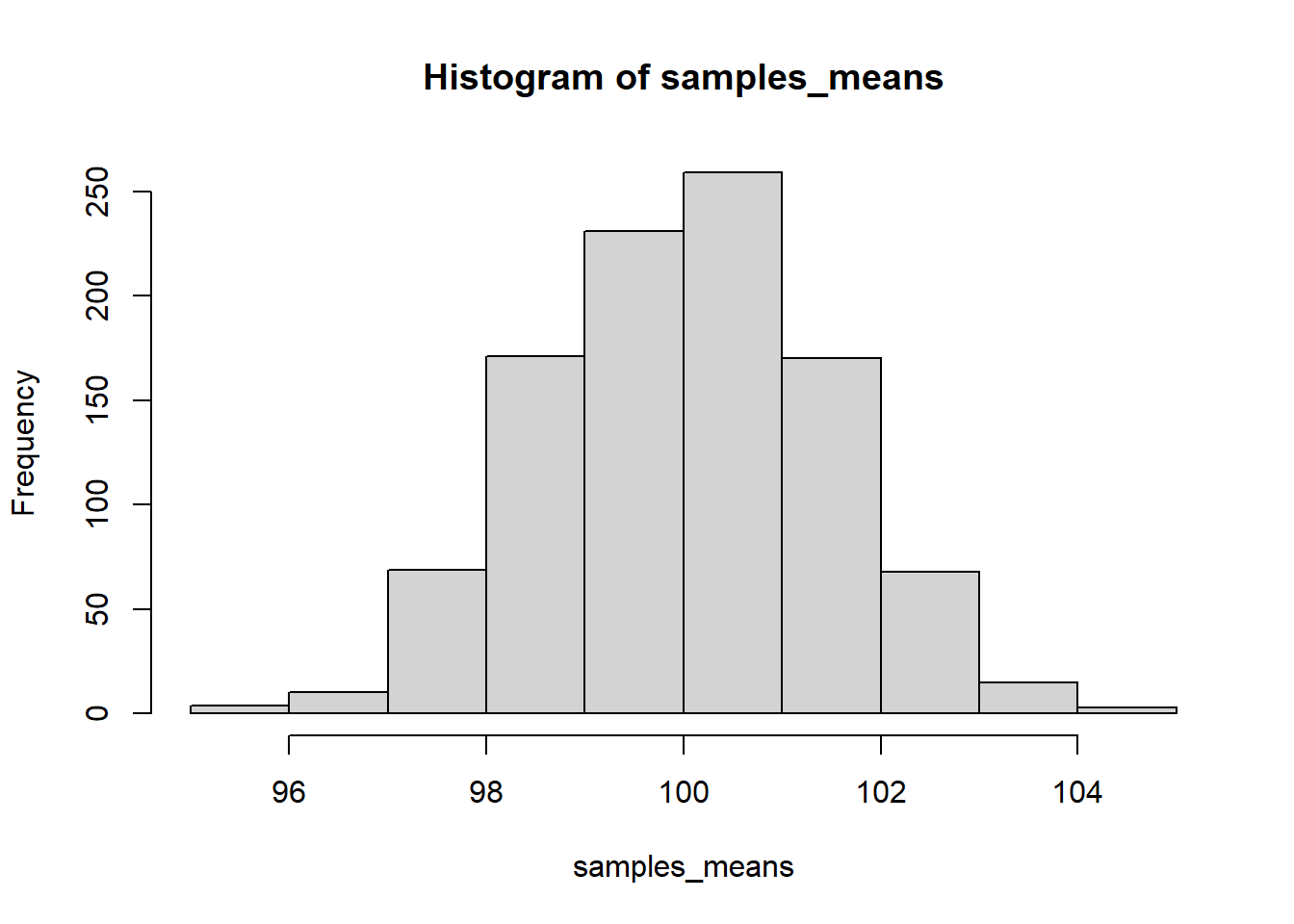
# 比较三种分布的横坐标与纵坐标。
# 总体分布。10000个个案的分布。
hist(
  Population10000$IQ,
  breaks = 10,
  xlim = c(40, 160)
)

# 样本分布。即，样本中100个个案的分布。
hist(sample1$IQ,
     breaks = 10,
     xlim = c(40, 160))

# 抽样分布。即，1000个样本的均值的分布。
hist(samples_means, 
     breaks = 10)

# 抽样分布的均值。即，1000个实际样本的均值的均值。
mean(samples_means)

[1] 100.0213

# 抽样分布的标准差。即，样本均值的标准误；
# 即，基于1000个实际样本的均值，计算1000个均值的标准差。
sqrt(sum((samples_means - mean(samples_means)) ^ 2) / 1000)

[1] 1.44925

# 使用总体标准差估计均值的标准误
15 / sqrt(100)

[1] 1.5

# 使用样本1的标准差估计样本1均值的标准误
sample1_sd_unbiased / sqrt(100)

[1] 1.414669

# 基于总体的标准差，对sample1的均值进行单样本z检验
z <- (sample1_mean - miu)/(delta/sqrt(100))
z

[1] -0.559083

# z的双尾p值
p_z <- pnorm(z)*2
p_z

[1] 0.5761051

# 基于sample1无偏标准差，对sample1的均值进行单样本t检验
t <- (sample1_mean - miu)/(sample1_sd_unbiased/sqrt(100))
t

[1] -0.592806

# t的双尾p值
p_t <- pt(t, 100 - 1)*2
p_t

[1] 0.5546627

# 采用R中的t.test函数对sample1的均值进行单样本t检验，结果与前文一致。
t.test.out <- t.test(sample1$IQ, alternative = "two.sided", mu = 100)
print(t.test.out)

    One Sample t-test

data:  sample1$IQ
t = -0.59281, df = 99, p-value = 0.5547
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
  96.35436 101.96839
sample estimates:
mean of x 
 99.16138